近似最近邻算法 HNSW 学习笔记（三）对于启发式近邻选择算法的一些看法

发表于 | 分类于 | 阅读次数：

前言

在 HNSW 中一大创新就是在选择连接的近邻时使用了启发式算法，在之后脱颖而出的近似最近邻算法 NSG 和 SSG （论文中提到是阿里巴巴正在使用的可用于十亿级别数据集的近似最近邻算法，表现出甚至优于 HNSW 的性能）中也采用了类似于其启发式的 RNG （不是那个 RNG 哦，顺便 LPL 加油！）算法来构建图。但是其启发式算法是比较难理解的，下面探探我的看法。

HNSW 文章：

Heuristic Select 启发式选择算法

在 HNSW 中，SEARCH-LAYER(q, ep, ef, lc) 返回 efConstruction 个最近邻点，我们知道 efConstruction 的值是大于 M 的，那么怎么在这些点中选择 M 个来进行双向连接呢？这时候就有一个选择算法了。论文中提出了两种选择算法：

  1. 简单选择算法 SELECT-NEIGHBORS-SIMPLE(q, C, M)
  2. 启发式选择算法 SELECT-NEIGHBORS-HEURISTIC(q, C, M, lc,...)

简单选择算法

简单选择算法非常简单，就是简单选择最近的 M 个进行连接。听上去我们第一感觉可能是，本来不就是应该选择最近的吗？难道还要选择更远的吗？别急，我们看看启发式搜索是怎么样的。

启发式选择算法

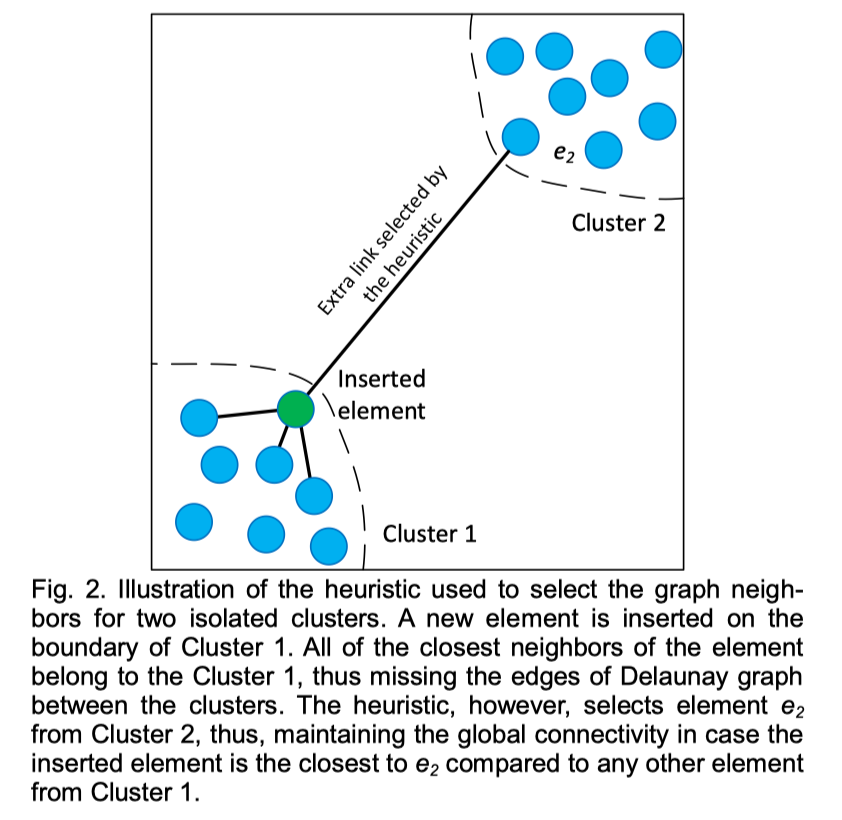
image-20190723153942371

论文中的图是这样的，我们可能会有疑惑，HNSW 的插入算法不是一个点一个点插入的吗，怎么会形成两个簇呢？其实论文中的图并不准确，实际上 HNSW 是可以保证图的全局连通性的。

数据的前几个结点插入以后可能是这样的：

image-20190723154734069

随着点的插入变多，可能变成这样：

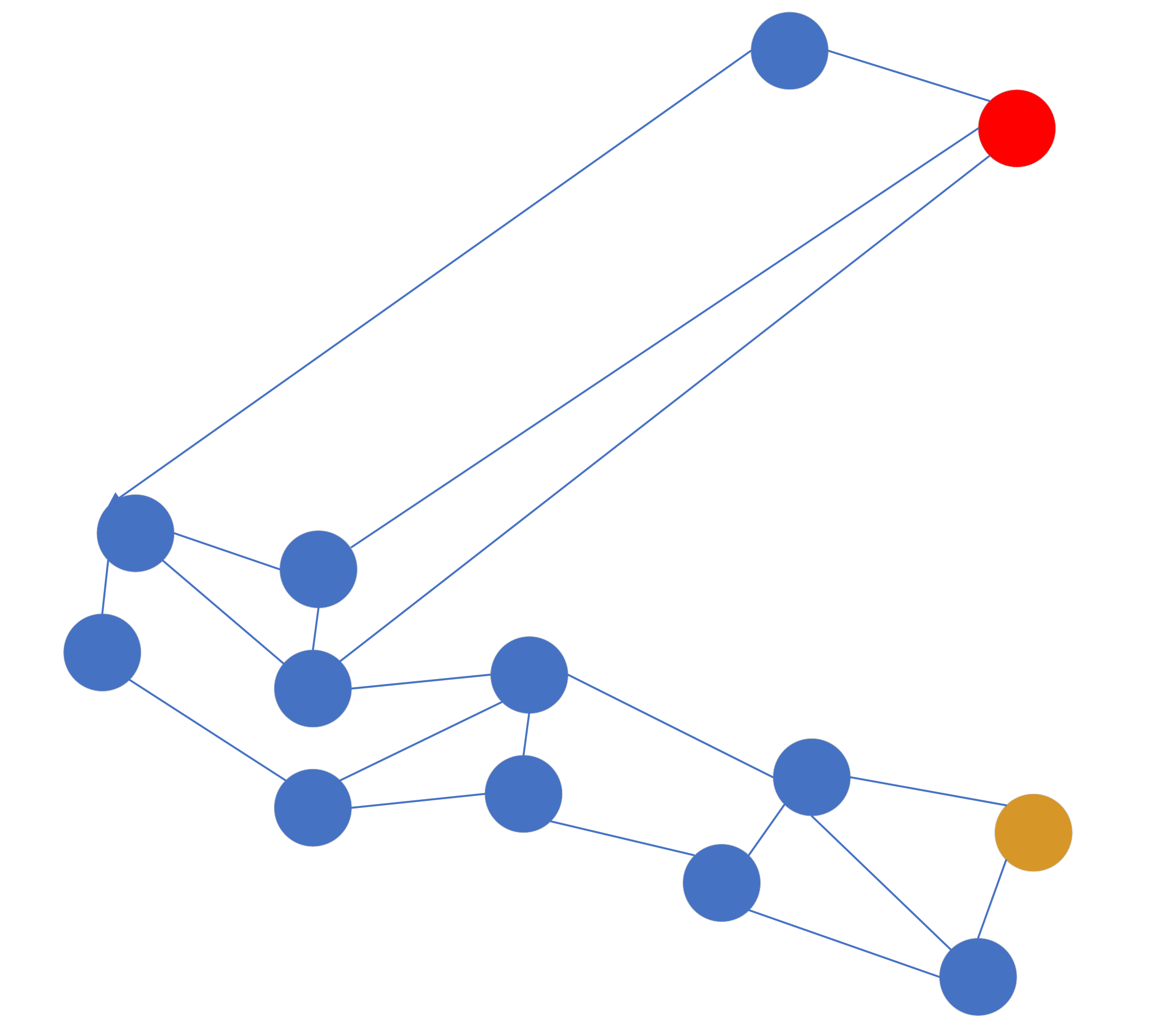
image-20190723155351746

这样的图可能不是很准确，但是可以说明问题，每个点之间的间隔代表向量之间的距离。这时候假设我们的入口点是黄色点，目标查询点是红色点，那么按照贪婪算法出来的路径方向是这样的：

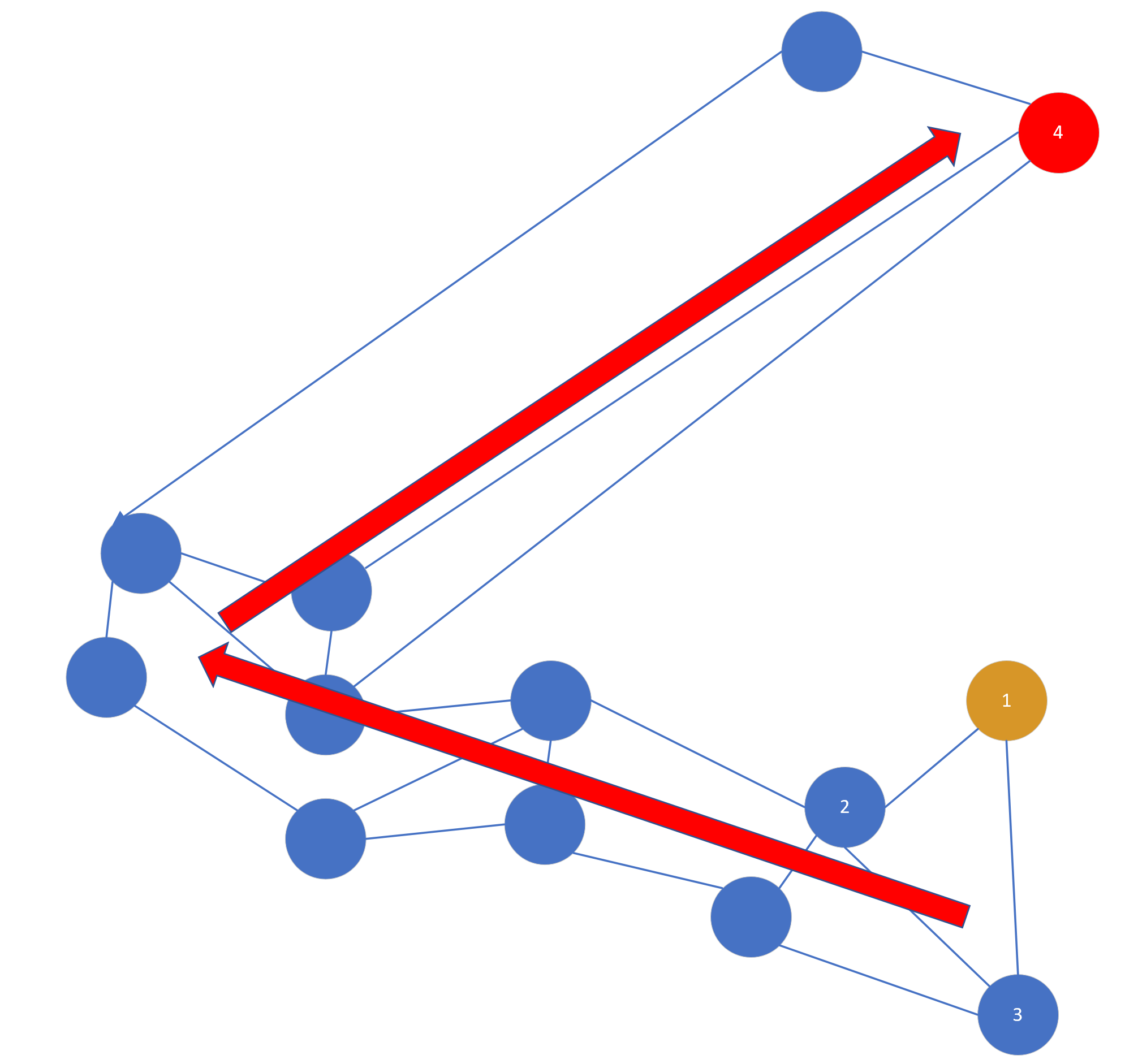
image-20190723160126763

可以看到这个路径是绕了一圈的，那么怎么可以更直接地到红点所在的区域呢，如果按照简单搜索算法，明显黄点和红点距离很远，在黄点周围有很多点可以连接，是永远轮不到红点的，但是如果使用启发式选择，他的选择办法是：当目标点（红点4）和插入点（黄点1）的距离比目标点（红点4）到任意一个插入点已经连接的点（2或3）近，就把目标点（红点4）和插入点（黄点1）连接起来。这句话很绕，其实就是，如果 距离（1，4）< 距离（2，4） 或 距离（1，4）< 距离（3，4） ，就连接 1 和 4，如图所示，当然图中的 link 很随性不一定严谨。

伪代码如下，注意关键部分：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
SELECT_NEIGHBORS_HEURISTIC(q, C, M, lc, extendCandidates, keepPrunedConnections)
/**
 * 输入
 * q：查询的点
 * C：候选元素集合
 * M：需要返回的数目
 * lc：层数
 * extendCandidates：指示是否扩展候选列表的标志
 * keepPrunedConnections：指示是否添加丢弃元素的标志
 */
Input: 
base element q, 
candidate elements C, 
number of neighbors to return M, 
layer number lc, 
flag indicating whether or not to extend candidate list extendCandidates, 
flag indicating whether or not to add discarded elements keepPrunedConnections
/**
 * 输出：探索得到M个元素
 */
Output: M elements selected by the heuristic

R ← ∅ // 记录结果
W ← C  // W：候选元素的队列
if extendCandidates  // 通过邻居来扩充候选元素
    for each e ∈ C
        for each e_adj ∈ neighbourhood(e) at layer lc
            if e_adj ∉ W
                W ← W ⋃ e_adj
Wd ← ∅  // 丢弃的候选元素的队列
/**
 * 这里是关键，他的意思就是：
 * 候选元素队列不为空且结果数量少于M时，在W中选择q最近邻e
 * 如果e和q的距离比e和R中的其中一个元素的距离更小，就把e加入到R中，否则就把e加入Wd（丢弃）
 * 可以理解成：如果R中存在点r，使distance(q,e)<distance(q,r)，则加入点e到R
 */
while │W│ > 0 and │R│ < M
    e ← extract nearest element from W to q
    if e is closer to q compared to any element from R
        R ← R ⋃ e
    else
        Wd ← Wd ⋃ e
/**
 * 如果设置keepPrunedConnections为true，且R不满足M个，那就在丢弃队列中挑选最近邻填满R为M个
 */
if keepPrunedConnections
    while │Wd│ > 0 and │R│ < M
        R ← R ⋃ extract nearest element from Wd to q
return R

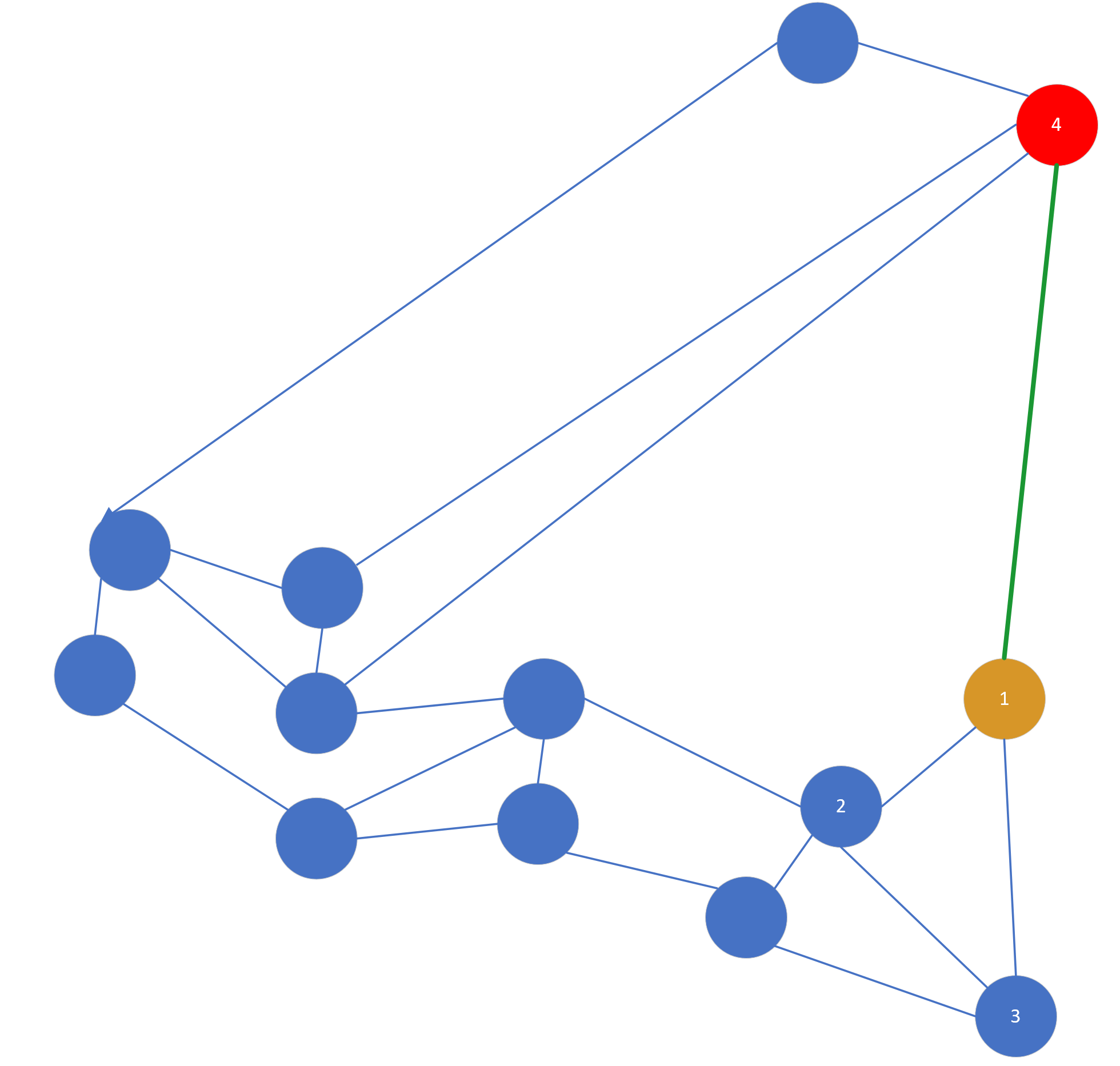
image-20190723160557230

这样 1 就可以直接查询到 4 所处的区域了，也就是说论文中的两簇数据。所以，启发式选择的目的不是为了解决图的全局连通性，而是为了有一条“高速公路”可以到另一个区域。

总结

以上就是我对 HNSW Heuristic Select 启发式近邻选择算法的一些看法，总的来说，启发式选择既考虑了结点之间的距离因素，也考虑了整个图不同区域的连通性，可以快速地查询到另一个区域，以减少了贪婪搜索的次数。

这也就是为什么增大 efConstruction 可以提升搜索效果了，如果 efConstruction 数值越接近 M , 那么启发式选择算法的效果越接近简单选择算法，当 efConstruction 设置足够大的时候，那么启发式选择算法才能发挥其作用，毕竟有些值得连接的点可不是真正最近的点。当然是不是 efConstruction 越大越好值得商榷。

这是我粗浅的个人理解，如果有不同的看法或者有什么疑惑欢迎发邮件 ryanligod@qq.com 或 ryanligod@gmail.com 和我讨论。

回复疑问

回复一下评论的提问，回复字数竟然有限制……

之前的理解有些偏差，我重新确认了一遍论文做了一些修改。

我的理解是：如果点插入的顺序不一样，那么最后构建的HNSW图索引是不一样的。如果插入的点是红点4，那么在进行启发式选择之前，会找到最近的 efConstruction 个点的一个集合W。

选择算法（简单选择或是启发式选择）的作用就是在集合 $W$ 中选择 M(M<efConstruction)​ 个点与“新插入点”进行连接。

按照代码来说的话，算法会遍历集合 $W$，遍历顺序是从距离红点4最近的点到最远的点。$W$ 中距离红点4最近的点$p_1$无论如何都会连接到红点4，接着第二个点 $p_2$ 就要要连接到点4得满足$distance(p_2,红点4)<distance(p_1,p_2)$，保证 $p_2$ 距离红点4比 $p_1$ 距离任意一个已经插入的点（目前只有 $p_1$）要近。遍历到W中的第三个点 $p_3$ 时，就得满足$distance(p_3,红点4)<distance(p_3,p_1)$ 或 $distance(p3,红点4)<distance(p3,p2)$。以此类推。

所以说红点4是不是能连接到黄点1是和当时已经被选择的点有关的，如果按照上面的图说，至少红点4旁边的那个店是会连接到红点4的（不过整个图也不一定严谨，主要了解思想），然后遍历到第二近的黄点1，发现黄点1和红点4的距离比黄点1与已经和红点4连接的那个点距离小，红点4就会连接黄点1。虽然说启发式选择算法不保证“插入点”连接最近的点，但是从全局来看，能保证和“插入点”连接的点是从 efConstruction 个最近的点里面选出来的。

0%